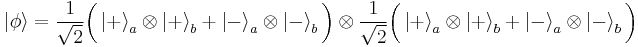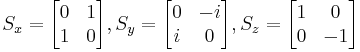Quantum pseudo-telepathy

This article uses quantum theoretical concepts and terminology. For a generally accessible introduction to quantum mechanics, see Introduction to quantum mechanics.
Quantum mechanics
\Delta x\, \Delta p \ge \frac{\hbar}{2}
Introduction
Glossary · History
Fundamental concepts
Complementarity · Decoherence
Duality · Ehrenfest theorem
Entanglement · Exclusion
Measurement · Probability amplitude
Nonlocality · Quantum state
Superposition · Tunnelling
Uncertainty · Wave function

Quantum pseudo-telepathy is a phenomenon in quantum game theory resulting in anomalously high success rates in coordination games between separated players. These high success rates would require communication between the players in a purely classical (non-quantum) world; however, the game is set up such that during the game, communication is physically impossible. Quantum pseudo-telepathy is often and easily misrepresented as paranormal[1], given that most people are not aware that the quantum laws of physics are subtly non-local and allow violations of Bell inequalities. This means that for quantum pseudo-telepathy to occur, prior to the game the participants need to share a physical system in an entangled quantum state, and during the game have to execute measurements on this entangled state as part of their game strategy. Games in which the application of such a quantum strategy leads to pseudo-telepathy are also referred to as quantum non-locality games.

In their 1999 paper,[2] Gilles Brassard, Richard Cleve and Alain Tapp demonstrated that winning quantum strategies can exist in simple games for which in the absence of quantum entanglement a winning strategy can result only if the participants were allowed to communicate. The term quantum pseudo-telepathy was later introduced[3] for this phenomenon. The prefix 'pseudo' is appropriate, as the quantum non-locality effects that are at the heart of the phenomenon do not allow any transfer of information, but rather eliminate the need to exchange information between the players for achieving a mutual win in the game.

The phenomenon of quantum pseudo-telepathy is mostly used as a powerful and explicit thought experiment of the non-local characteristics of quantum mechanics. Yet, the effect is real and subject to experimental verification, as demonstrated by the experimental confirmation of the violation of the Bell inequalities.

Contents

The Mermin-Peres magic square game

An example of quantum pseudo-telepathy can be observed in the following two-player coordination game in which the participants fill one row and one column of a 3x3 table with plus and minus signs.

The two players Alice and Bob are separated so that no communication between them is possible. In each round of the game Alice gets informed which row is selected, and Bob is being told which column is selected. Alice does not get to know the column Bob has been presented with, and vice versa (Bob remains unaware of the row presented to Alice). Alice and Bob both have to put the same sign in the cell common to the row and column selected. Furthermore (and this is the catch), Alice has to fill the remainder of the row such that there is an even number of signs in that row, whilst Bob has to fill the remainder of the column such that there is an odd number of signs in that column.

It is easy to see that any prior agreement between Alice and Bob on the use of specific tables filled with + and – signs is not going to help them. The reason being that such tables simply do not exist: as these would be self-contradictory with the sum of the minus signs in the table being even based on row sums, and being odd when using column sums.

So, how can Alice and Bob succeed in their task?

The trick is for Alice and Bob to share an entangled quantum state and to use specific measurements on their components of the entangled state to derive the table entries. A suitable correlated state consists of a pair of Bell states:

\left|\phi\right\rang = \frac{1}{\sqrt{2}} \bigg(\left|%2B\right\rang_a \otimes \left|%2B\right\rang_b %2B \left|-\right\rang_a \otimes \left|-\right\rang_b \bigg) \otimes \frac{1}{\sqrt{2}} \bigg(\left|%2B\right\rang_a \otimes \left|%2B\right\rang_b %2B \left|-\right\rang_a \otimes \left|-\right\rang_b \bigg)

here |+> and |-> are eigenstates of the Pauli operator Sz with eigenvalues +1 and −1, respectively, whilst the subscripts a and b denote which component of each Bell state is going to Alice and which one goes to Bob.

Observables for these components can be written as products of the Pauli spin matrices:

S_x = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} , S_y = \begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix} , S_z = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}

Products of these Pauli spin operators can be used to fill the 3x3 table such that each row and each column contains a mutually commuting set of observables with eigenvalues +1 and −1, and with the product of the obervables in each row being the identity operator, and the product of observables in each column equating to minus the identity operator. This so-called Mermin-Peres magic square[4] is shown in below table.

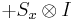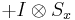%2BS_x \otimes I %2BS_x \otimes S_x %2BI \otimes S_x
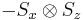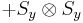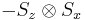-S_x \otimes S_z %2BS_y \otimes S_y -S_z \otimes S_x
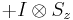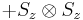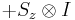%2BI \otimes S_z %2BS_z \otimes S_z %2BS_z \otimes I

Effectively, while it is not possible to construct a 3x3 table with entries +1 and −1 such that the product of the elements in each row equals +1 and the product of elements in each column equals −1, it is possible to do so with the richer algebraic structure based on spin matrices.

Current research

It has been demonstrated[5] that the above described game is the simplest two-player game in which quantum pseudo-telepathy can occur. Other games in which quantum pseudo-telepathy occurs have been studied, including larger magic square games,[6] graph colouring games[7] giving rise to the notion of quantum chromatic number[8], and multiplayer games involving more than two participants.[9] Recent studies tackle the question of the robustness of the effect against noise due to imperfect measurements on the coherent quantum state.[10]

See also

Notes

  1. ^ http://www.science20.com/hammock_physicist/telepathy_and_quantum_0
  2. ^ Gilles Brassard, Richard Cleve, Alain Tapp, "The cost of exactly simulating quantum entanglement with classical communication" (1999).
  3. ^ Gilles Brassard, Anne Broadbent, Alain Tapp, "Multi-Party Pseudo-Telepathy" (2003).
  4. ^ Here we use the table as defined in: P.K. Aravind, "Quantum mysteries revisited again", American Journal of Physics. 72, 1303-7 (2004).
  5. ^ Nicolas Gisin, Andre Allan Methot, Valerio Scarani, "Pseudo-telepathy: input cardinality and Bell-type inequalities" (2006).
  6. ^ Samir Kunkri, Guruprasad Kar, Sibasish Ghosh, Anirban Roy, "Winning strategies for pseudo-telepathy games using single non-local box" (2006).
  7. ^ David Avis, Jun Hasegawa, Yosuke Kikuchi and Yuuya Sasaki, "A quantum protocol to win the graph colouring game on all Hadamard graphs" (2005).
  8. ^ Peter J. Cameron, Ashley Montanaro, Michael W. Newman, Simone Severini, Andreas Winter, "On the quantum chromatic number of a graph" Electronic Journal of Combinatorics 14(1), 2007.
  9. ^ Gilles Brassard, Anne Broadbent, Alain Tapp, "Recasting Mermin's multi-player game into the framework of pseudo-telepathy" (2004).
  10. ^ P. Gawron, J.A. Miszczak, J. Sladkowski, "Noise Effects in Quantum Magic Squares Game", International Journal of Quantum Information, Vol. 6, No. 1 (2008), pp. 667 - 673.